Force Distribution on the Threads of a Screw in Bolted Connections

Every now and then every Structural Engineer has to asses fasteners against thread ripping, especially when non standard screws are used.

In fact, in general, handbooks give the tightening torque for every nominal diameter and the load that the bolt can whithstand, assuming that both the screw and the nutscrew are made of steel.
In Chapter 1 of the book Computational Structural Engineering an axisymmetric model of an M18 thread is presented to show a possible usage of axisymmetric elements.

Here the same model is used to show something that is already well known: the force distribution is not uniformely distrbuted on the threads.

What is not well known is how much force sees the most loaded thread.

The topic is far from being trivial and it is not easy to find something reliable in literature, although some numbers could be retrieved from a book from 1943!

So the opportunity to run the model with both the screw and the nutscrew in steel and with the screw in steel and the nutscrew in aluminium was taken.

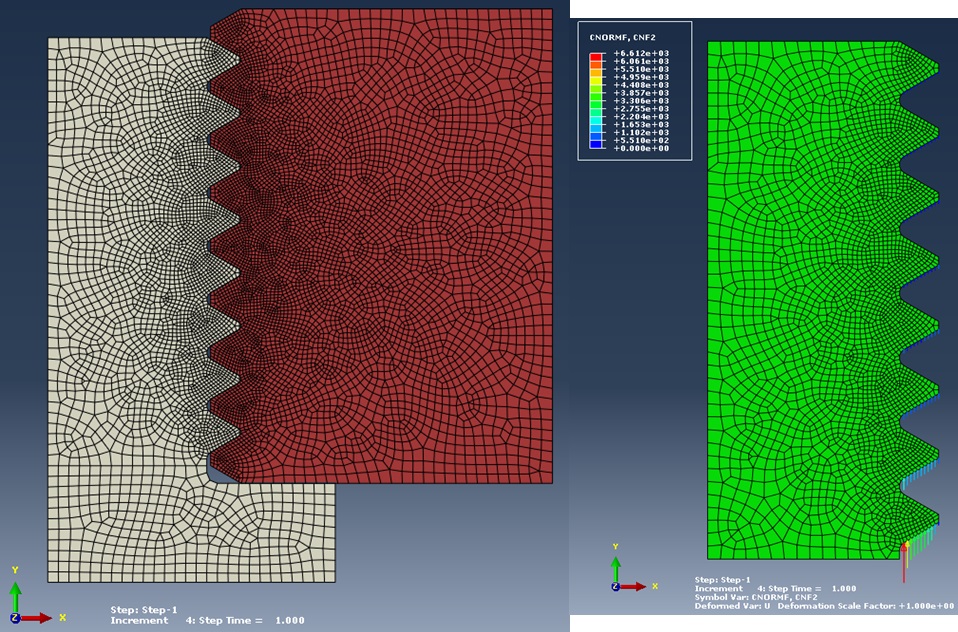
Additionally, for the steel-steel case, the elastic-plastic behavior was considered for jus the screw; the model is the same for all the three cases and it is shown in the first picture (on the left).

Then for all the models the forces acting on the first six threads were extracted (first picture on the right shows the nodal forces acting on the threads).

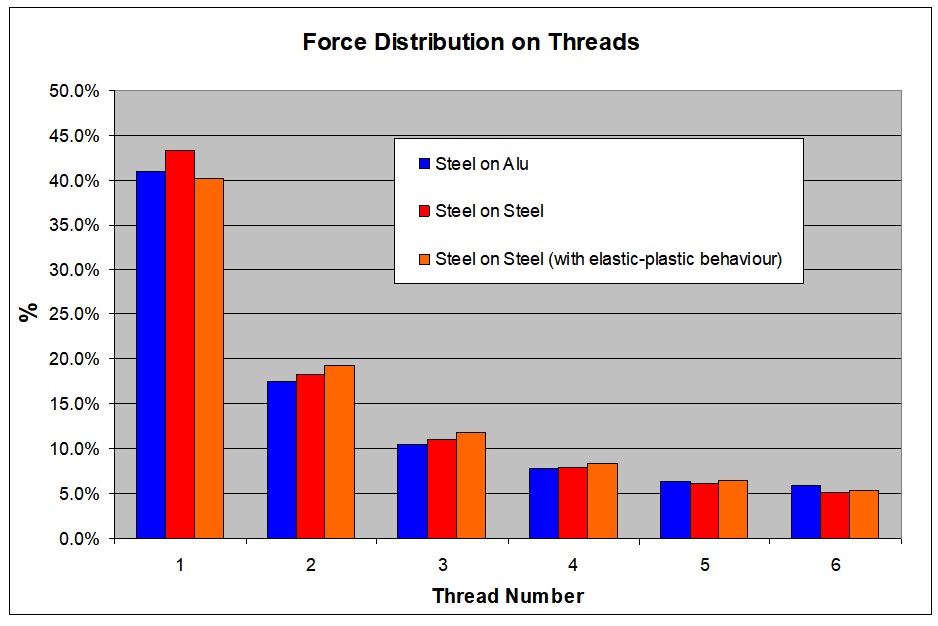
Results are collected into the Excel graphic shown in the second picture, where it is possible to see that the aluminium nutscrew, due to the higher compliance, gives a more even distribution, with respect to the steel-steel case.

Interesting to note that the non linear behavior of the steel is giving a similar effect, thus reducing the load on the first thread.

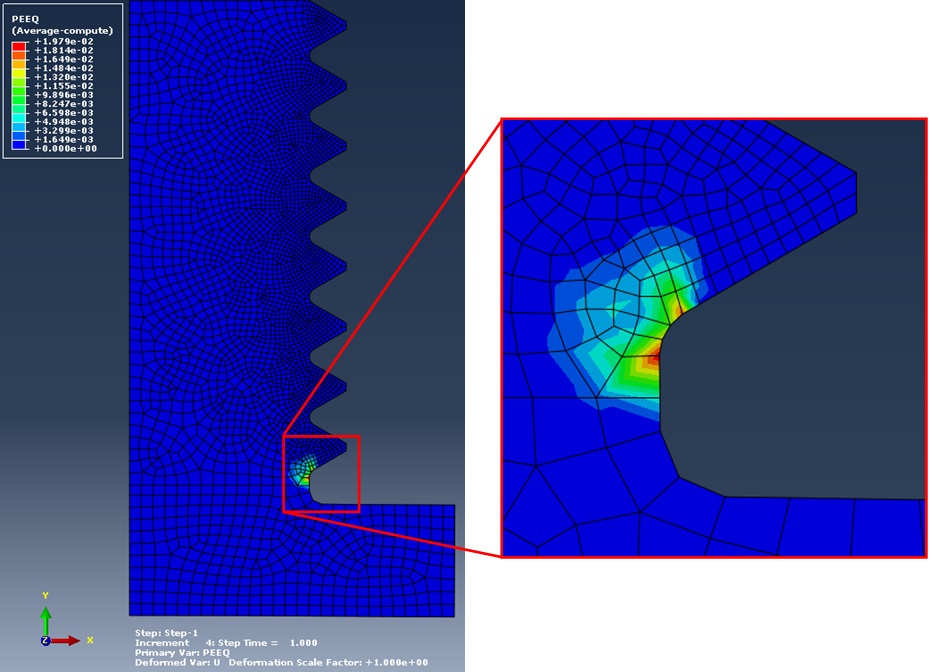
The material considered is a 8.8 steel class, meaning that Rt is 800 MPa and yield is at 0.8×800 = 640 MPa. The third picture shows that a small plasticization (1.97%) occurs in a small area of the first thread in the screw, by just applying the nominal preload taken from some design standards.

This fact is enough to unload the first thread, thus coming to an intermediate situation between steel-steel with no plasticization and steel-aluminium. On the other threads the load tends to be bigger than both cases, but anyway what matters is the most loaded one: if this resists, also the others will.