HEX8 vs TET10 Elements: the everlasting debate
I think I am not exaggerating if I say that worldwide the FEA community recognizes that the “best” element type for 3D structures is the hexahedron element (the so-called brick element), especially in its linear formulation (linear shape functions – 8 nodes per element), where with “best” I mean the optimal compromise between model size and quality of the results.
Nonetheless obtaining brick meshes is not straightforward at all; automatic meshers are not capable to obtain a full brick mesh and partitioning solids into hexahedral volumes it’s not an easy task, that sometimes becomes definitely impossible if the geometry is really complex.
TET10 elements are quadratic (in the sense that their shape functions are second order polynomials) and they do represent a very good alternative to HEX8 because they’re suitable for automatic meshers.
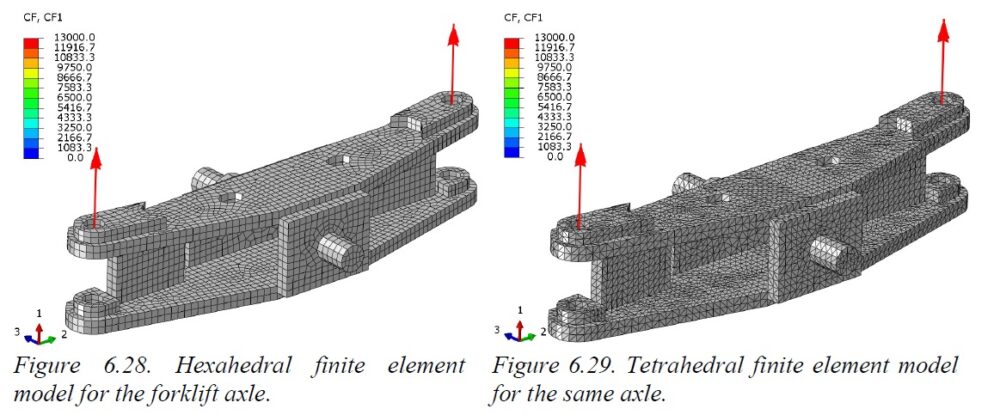
The pictures here shown are taken from Chapter 6 of the book “Computational Structural Engineering” and they document a comparison between two models with the same mesh size: one is built with HEX8 elements and the other with TET10 elements (the part is the axle of a forklift truck).
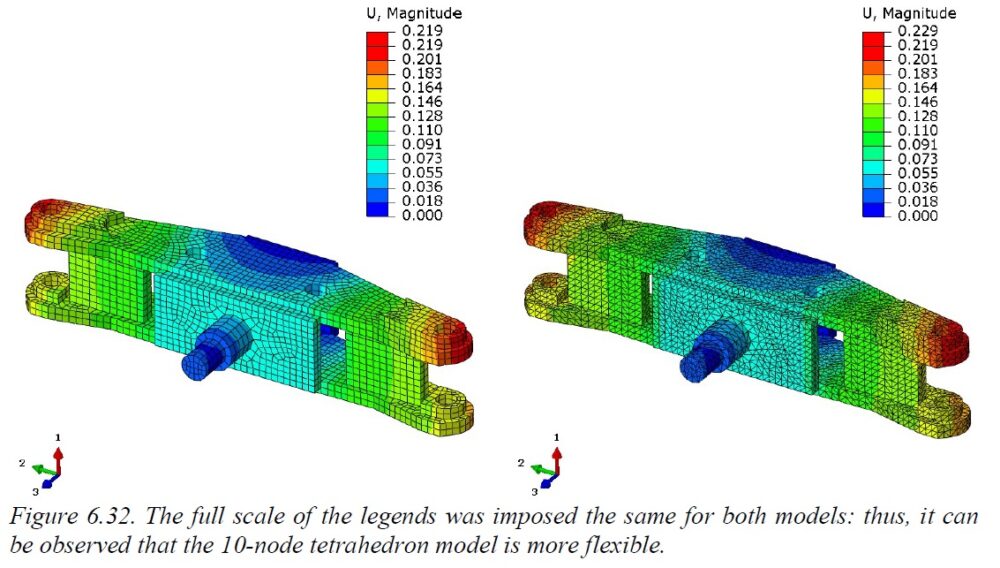
In terms of displacements the TET10 model appears slightly softer (a difference <5% could be considerered negligible from an engineering point of view and it would anyway be necessary to investigate a little more to find where this difference is coming from)
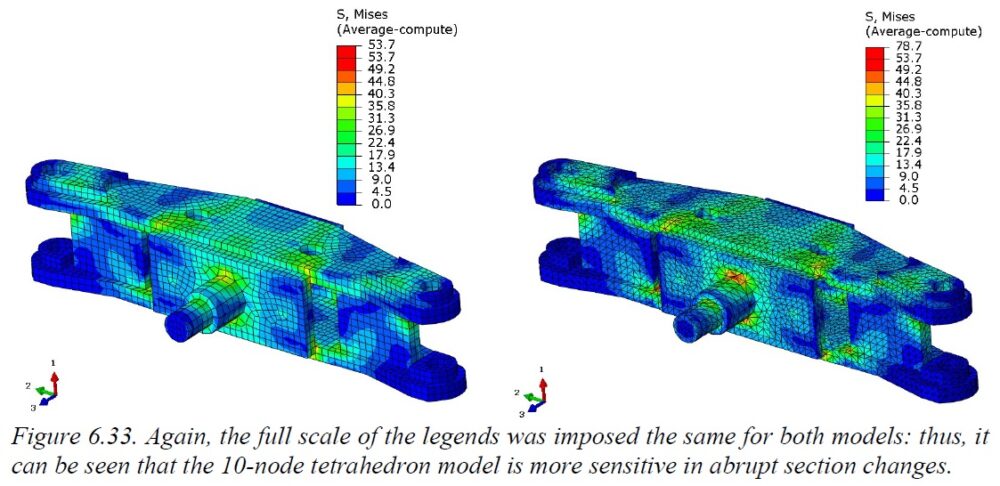
By imposing the same stress limits in the legend of the contours for the two models, we realize that the TET10 model is more sensitive to abrubt geometry changes. Nevertheless, a part from the mentiones areas, the contours are comparable.
Everything them seems fine: the TET10 model can be easily obtained by automatic meshers and the results it provides is in line with what a HEX8 model produces. However all this has a cost, as it can be seen from the table here below: despite the mesh size of the two models is practically the same, the number of elements is about 8 times bigger in the TET10 model; similar speech for the number of nodes and the size of the result file.

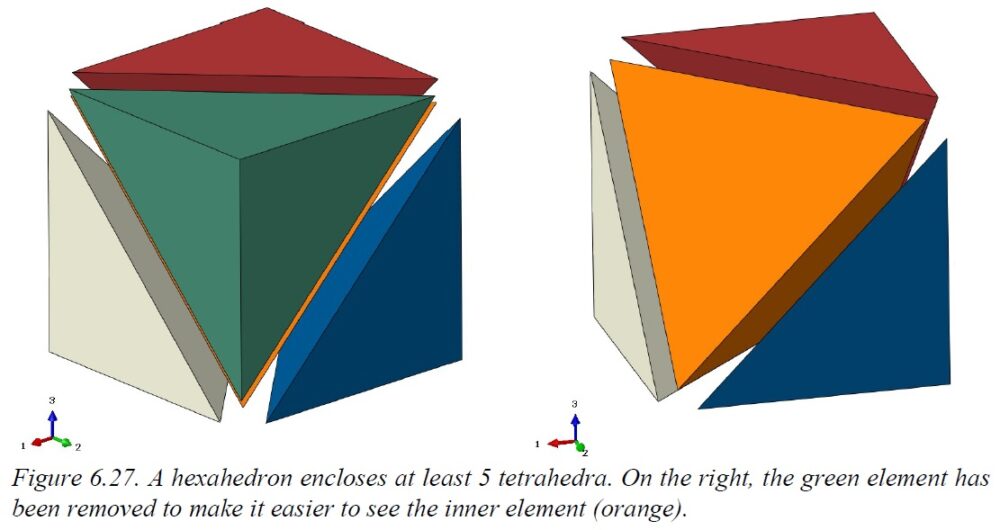
This happens because a hexahedron can contain at minimum 5 tetrahedron, as shown here below.
All this is reflected on the solution times, that in turns means more CPU commitment and therefore more energy consumption.
